3月25日，哲學(xué)系馬明輝教授指導(dǎo)邏輯學(xué)專業(yè)本科生陳謙在國際符號(hào)邏輯雜志Studia Logica發(fā)表論文“Lattices of Finitely Alternative Normal Tense Logics”。論文研究有窮可擇時(shí)態(tài)邏輯T(m,n)正規(guī)擴(kuò)張格的邏輯性質(zhì)，準(zhǔn)確描述了T(1,1)正規(guī)擴(kuò)張格的結(jié)構(gòu)：

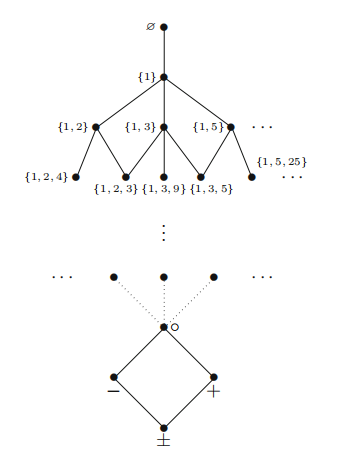
證明了T(1,1)正規(guī)擴(kuò)張格中存在可數(shù)多個(gè)不具有有窮模型性質(zhì)的時(shí)態(tài)邏輯，存在不多數(shù)多個(gè)不是有窮可公理化的邏輯，有且僅有一個(gè)瀕表格邏輯。對(duì)任意自然數(shù)n,m使得nm大于等于2，時(shí)態(tài)邏輯T(n,m)正規(guī)擴(kuò)張格中存在不可數(shù)多個(gè)不具有有窮模型性的邏輯，存在不可數(shù)多個(gè)瀕表格邏輯。這一系列結(jié)論，充分說明了正規(guī)時(shí)態(tài)邏輯格與正規(guī)模態(tài)邏輯格的巨大差異，明確了研究正規(guī)時(shí)態(tài)邏輯的重要意義。

學(xué)術(shù)雜志Studia Logica是波蘭科學(xué)院主辦的刊物，主要刊載運(yùn)用當(dāng)代形式邏輯方法研究邏輯系統(tǒng)的成果，例如代數(shù)、模型論、證明論等等，以及一般性的邏輯理論和邏輯在哲學(xué)、科學(xué)方法、語言學(xué)等分支的應(yīng)用成果。

論文鏈接：https://link.springer.com/article/10.1007/s11225-021-09942-5